| | |
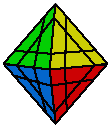
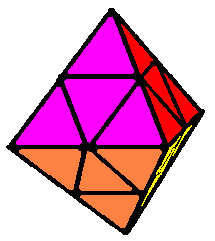
The setup of the octahedron is distributed into 6 corners with each four sides / four colors and eight center stones, which carry only on clor each.
The center stones are separated into two four-groups, which rotate solitare, without interacting with each other. It does not play a role for solution, just fine to know it.
The corners can be moved in a three cycle. Is the first slice soluted, this is equalent with a cycle of three center stones, anticycling to the cycle sense of the corners.
A four-swap is possible too, but can be described as a 180° rotation of two corners, which are opponing them selve in space.
To honor my personal view of the octahedron I'm using it in some cases as a right and in other cases as a left handed parallelogramm. This is shown through those both symbols:
  
Because there are in both views two front slices I'm using a standing and a skipped triangle to show which plate is used:
  
If in a sequence an arrow is different from this "note key" it is supplied with an own triangle, like a foot note:
 
After that the note key from the start is working again.
To the inner construction of the octahedron: A group of four center stones form a fix tetrahedron cross, it is this similar to that of the Rubik's Cube with its center stones. Those center stones here are turnable too, them and the four others, which are free moveable, can be oriented in three directions, each differing about 120°.
Between the fix center stones are the six corners enhanced, and those hold the four moveable center stones.
Who wants to know which center stones are fix and which moveable, presses the thumb on those eight triangles. The four moveables can be pressed by some millimeters, the fix ones don't react.
| | | |
Der Aufbau des Oktaeders ist unterteilt in 6 Ecken mit vier Seiten / vier Farben und in acht Mitten, die nur eine Farbe tragen.
Die Mitten bilden zwei Vierer-Gruppen, die unabhängig voneinander rotieren können, ohne sich gegenseitig zu beeinflussen. Dies spielt beim Lösen keine Rolle, nur gut, es zu wissen.
Die Ecken können in einem Dreiertausch bewegt werden. Ist die erste Schicht bereits gelöst, so ist dieser gleich zu setzen mit einem Zyklus dreier Mittelsteine, dieser der Bewegungsrichtung der Ecken entgegengesetzt.
Auch ein Vierertausch ist möglich, läßt sich aber auch als 180°-Drehung zweier Mittelsteine beschreiben, die einander gegenüber liegen.
Um meiner eigenen Perspektive des Oktaeders Gebühr zu erweisen, verwende ich ihn in manchen Fällen als rechts- und in anderen Fällen als linksgerichtete Raute. Dies wird durch diese beiden Symbole angezeigt:
  
Da es in beiden Ansichten immer zwei vordere Scheiben gibt, verwende ich ein stehendes und ein gekipptes Dreieck, um anzuzeigen, welche Fläche verwendet wird:
  
Sollte ein in einer Folge vorkommender Pfeil von diesem "Notenschlüssel" abweichen, wird er wie hier als "Fußnote" mit einem Dreieck versehen:
 
Anschließend gilt wieder der "Notenschlüssel" von Beginn an.
Zur Konstruktion des Oktaeders: Eine Gruppe von vier Mittelsteinen bildet ein starrers Tetraeder-Kreuz, es entspricht so dem Achsenkreuz des Rubik's Cube mit seinen Mittelsteinen. Auch sind diese Mittelsteine drehbar, sie und die vier anderen, die beweglich sind, können je drei Positionen annehmen, jede um 120° verschieden.
Zwischen den starren Mittelsteinen sind die sechs Ecken eingehängt, und diese wiederum halten die vier beweglichen Mittelsteine.
Wer wissen will, welche Mittelsteine starr, und welche beweglich verankert sind, muß nur etwas Druck auf diese acht Dreiecke ausüben. Die vier starren lassen sich nicht eindrücken, die vier anderen, beweglichen, geben etwas nach.
| | |