                                 |
 Ecken negativ drehen, alle Kanten wenden - Kantentausch Ecken negativ drehen, alle Kanten wenden - Kantentausch  twisting corners negative, flipping all edges - permuting edges twisting corners negative, flipping all edges - permuting edges |
 |
                                                           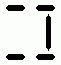  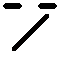  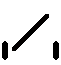  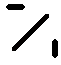  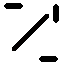  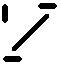  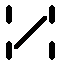  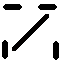  |
 |
                                          |
 |
                                       |
 |
                                   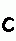 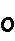 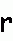 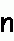  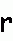 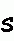  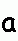 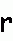   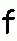    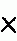  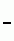  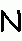              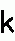  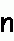  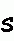    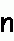   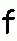  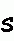     |
 |
          |
 |
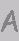     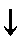  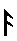  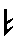    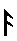      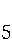     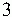  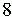     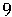     |
   M U' r U² r' U' R U' r R² (11,15) M U' r U² r' U' R U' r R² (11,15) |
       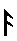  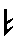  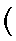   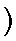  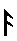     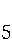     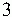  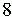          |
 r' (R U') r U² r' U' (R U') R² r (11,15) r' (R U') r U² r' U' (R U') R² r (11,15) |
                                  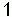     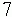             |
   f · R U R' U' · f' U F · R U R' U' F' (13) BobBurton OLL 12 f · R U R' U' · f' U F · R U R' U' F' (13) BobBurton OLL 12 |
  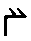 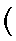     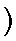 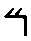                        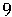     |
 f (R U R' U') f' U F (R U R' U') F' (13) f (R U R' U') f' U F (R U R' U') F' (13) |
         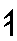 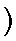  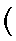 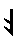       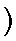 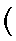    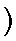           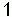              |
   (L (L' M') U' (L M) U² (L' M') U') (L U' L²) R (11,13) Peter Jansen (L (L' M') U' (L M) U² (L' M') U') (L U' L²) R (11,13) Peter Jansen |
                           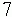  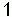      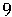     |
 F U R U' R' F' L F U F' U' L' (12,12) Ron van Bruchem F U R U' R' F' L F U F' U' L' (12,12) Ron van Bruchem |
  |
              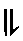 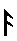          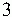  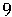          |
 r' R U' r U² r' U' R U' R²' r (9,13) Dan Harris r' R U' r U² r' U' R U' R²' r (9,13) Dan Harris |
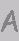                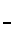           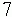  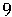     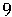     |
 R - L' B' L U² L' B' - R B' R² - L (9,13) R - L' B' L U² L' B' - R B' R² - L (9,13) |
            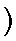  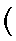 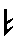 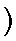  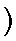 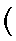    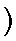           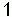 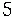  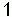      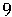     |
 (R (R' M) U' (R M') U² (R' M) U') (R U' R²) L (11,13) Peter Jansen (R (R' M) U' (R M') U² (R' M) U') (R U' R²) L (11,13) Peter Jansen |
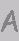                      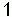 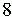  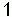      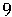     |
 l L² U' L U' l' U² l U' M' (10,13) Peter Jansen l L² U' L U' l' U² l U' M' (10,13) Peter Jansen |
                         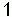      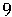     |
 R U B U' B' R' F R U R' U' F' (12) Jessica Fridrich R U B U' B' R' F R U R' U' F' (12) Jessica Fridrich |
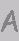                       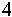  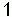      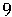     |
 Rs B' L U² L' B' R B' R²'L (10,13) Jessica Fridrich Rs B' L U² L' B' R B' R²'L (10,13) Jessica Fridrich |
                                       |
 F' U² F' L F L' U' L' U' L U' F (12,13) Jessica Fridrich F' U² F' L F L' U' L' U' L U' F (12,13) Jessica Fridrich |
                                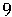     |
 r' R U' r U² r' U' R U' R² r (11,13) Dennis Nilsson r' R U' r U² r' U' R U' R² r (11,13) Dennis Nilsson |
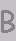      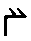                                 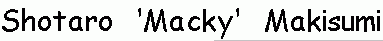  |
 Fw R U R' U' Fw' - U - F R U R' U' F' (13) Shotaro Macky Makisumi Fw R U R' U' Fw' - U - F R U R' U' F' (13) Shotaro Macky Makisumi |
               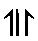           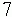  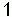      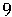     |
 y R' L F' R U² R' F' L F' RL²' (11,13) Ron van Bruchem y R' L F' R U² R' F' L F' RL²' (11,13) Ron van Bruchem |
           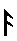   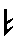                  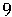     |
 r R² U' R U' r' U² r U' R r' (10,12) Dennis Nilsson r R² U' R U' r' U² r U' R r' (10,12) Dennis Nilsson |
    |
 |
 |