   F²'B² UD' R²'L² U'D (4,12) F²'B² UD' R²'L² U'D (4,12) |
                                             |
   F² R² F²'B² R² B² (5,12) F² R² F²'B² R² B² (5,12) |
                                                |
   U F'B' R'L' F'B' RL FB RL U' (8,14) U F'B' R'L' F'B' RL FB RL U' (8,14) |
                                                |
   U F² U² F² RL B² D² B² U² R'L' U (11,20) U F² U² F² RL B² D² B² U² R'L' U (11,20) |
                                                |
   U FB RL FB R'L' F'B' R'L' U' (8,14) U FB RL FB R'L' F'B' R'L' U' (8,14) |
                                                |
   U FB U² R² D² R² F'B' L² U² L² U (11,20) U FB U² R² D² R² F'B' L² U² L² U (11,20) |
                                                       |
   F R' U B² L' F UD' L' B R² U' F L' U'D (14,18) F R' U B² L' F UD' L' B R² U' F L' U'D (14,18) |
                                                           |
   F U' F R' D F' D F' RL B' U B' U L' B D' B UD (18,20) F U' F R' D F' D F' RL B' U B' U L' B D' B UD (18,20) |
                                                  |
   F² R FB' D B² D' F²'B² U F² U' FB' R' B² (13,22) F² R FB' D B² D' F²'B² U F² U' FB' R' B² (13,22) |
                                                        |
   F R F D' F'B R F' U' B' RL' F U'D' F'B' R² U (15,20) F R F D' F'B R F' U' B' RL' F U'D' F'B' R² U (15,20) |
                                                  |
   U F'B' R F² UD' L² F' U'D' F² R' U'D RL' D² (13,22) U F'B' R F² UD' L² F' U'D' F² R' U'D RL' D² (13,22) |
                                                          |
   F R D R' F' U B' L U'D L' F D' B R U' R' B' (17,18) F R D R' F' U B' L U'D L' F D' B R U' R' B' (17,18) |
                                                      |
   F R' B R'L U' RL' U B RL' D' B' L F' (13,16) F R' B R'L U' RL' U B RL' D' B' L F' (13,16) |
                                                |
   F R² F² U'D R' U²'D² L' F² L² U'D F (11,20) F R² F² U'D R' U²'D² L' F² L² U'D F (11,20) |
                                                     |
   F R'L' U' FB' R' L F² U² FB D' RL U² B' (12,20) F R'L' U' FB' R' L F² U² FB D' RL U² B' (12,20) |
                                                 |
   F U² F²'B² R'L F² U F²'B² U F² RL' D² F (12,24) F U² F²'B² R'L F² U F²'B² U F² RL' D² F (12,24) |
                                                          |
   U FB' U' R F' R' B R' U² R' F R' B' R U' F'B U (17,20) U FB' U' R F' R' B R' U² R' F R' B' R U' F'B U (17,20) |
                                                  |
   U F² R'L' F D² R'L B² D' F'B' R' UD' R'L U² (13,22) U F² R'L' F D² R'L B² D' F'B' R' UD' R'L U² (13,22) |
                                                     |
   FB R F² U'D R² B' U'D' L' UD' R'L U R² (12,20) FB R F² U'D R² B' U'D' L' UD' R'L U R² (12,20) |
                                             |
   FB UD R²'L² UD FB (5,12) FB UD R²'L² UD FB (5,12) |
                                        |
   U²'D² (2,4) U²'D² (2,4) |
                                                 |
   U FB R² UD F'B U'D' R² F'B' D' (9,16) U FB R² UD F'B U'D' R² F'B' D' (9,16) |
                                                |
   U FB D² R² D² R² F'B' R² D² R² U (11,20) U FB D² R² D² R² F'B' R² D² R² U (11,20) |
                                                 |
   U F'B' R² U'D' FB' UD R² FB D' (9,16) U F'B' R² U'D' FB' UD R² FB D' (9,16) |
                                                |
   U F² D² F² RL F² D² F² D² R'L' U (11,20) U F² D² F² RL F² D² F² D² R'L' U (11,20) |
                                              |
   F² R² F²'B² R² B² U²'D² (6,16) F² R² F²'B² R² B² U²'D² (6,16) |
                                            |
   F²'B² UD' R²'L² UD' (4,12) F²'B² UD' R²'L² UD' (4,12) |
                                                |
   U FB R'L' FB R'L' FB R'L' U' (8,14) U FB R'L' FB R'L' FB R'L' U' (8,14) |
                                                |
   U FB D² R² U² R² F'B' L² D² L² U (11,20) U FB D² R² U² R² F'B' L² D² L² U (11,20) |
                                                |
   U F'B' RL F'B' RL F'B' RL U' (8,14) U F'B' RL F'B' RL F'B' RL U' (8,14) |
                                                |
   U F² D² F² RL B² U² B² D² R'L' U (11,20) U F² D² F² RL B² U² B² D² R'L' U (11,20) |
                                                     |
   F R'L' U' L² B² R L F'B R'L D' RL U² F' (12,20) F R'L' U' L² B² R L F'B R'L D' RL U² F' (12,20) |
                                                     |
   F U² F²'B² RL' B² U' R²'L² U F² RL' D² B' (12,24) F U² F²'B² RL' B² U' R²'L² U F² RL' D² B' (12,24) |
                                                      |
   F R² D F' U' R U²'D² L' U B D' L² B' (13,18) F R² D F' U' R U²'D² L' U B D' L² B' (13,18) |
                                                          |
   F U R' U L' U' L D RL U R D' R' D L' D B (17,18) F U R' U L' U' L D RL U R D' R' D L' D B (17,18) |
                                                 |
   FB R F² U'D R² B' U'D' R' U'D RL' D L² (12,20) FB R F² U'D R² B' U'D' R' U'D RL' D L² (12,20) |
                                                        |
   F R' F'B L' F U' FB U² FB U' R' B RL' F R' (15,20) F R' F'B L' F U' FB U² FB U' R' B RL' F R' (15,20) |
                                                  |
   U F'B' R F² UD' L² F' U'D' F² R' U'D RL' U² (13,22) U F'B' R F² UD' L² F' U'D' F² R' U'D RL' U² (13,22) |
                                                         |
   F U' R B R FB' U' F U'D L' D RL' B² R' U F' (16,20) F U' R B R FB' U' F U'D L' D RL' B² R' U F' (16,20) |
                                                  |
   F² R FB' D B² U' R²'L² D B² U' F'B L' F² (13,22) F² R FB' D B² U' R²'L² D B² U' F'B L' F² (13,22) |
                                                       |
   F R² U' R U F' UD' L U' F' U F² L' UD' (14,18) F R² U' R U F' UD' L U' F' U F² L' UD' (14,18) |
                                                        |
   F R' F'B L' F U FB U² FB U L' F R'L B L' (15,20) F R' F'B L' F U FB U² FB U L' F R'L B L' (15,20) |
                                                 |
   FB' R FB D L² FB' U² L' UD R² F²B' RL' (12,22) FB' R FB D L² FB' U² L' UD R² F²B' RL' (12,22) |
                                                        |
   FB' U R D B' UD' R D' F' D' R B² U'D' R'L' U (15,20) FB' U R D B' UD' R D' F' D' R B² U'D' R'L' U (15,20) |
                                                  |
   U F² R'L' F D² R'L B² D' F' B' R' UD' R'L D² (13,22) U F² R'L' F D² R'L B² D' F' B' R' UD' R'L D² (13,22) |
                                             |
   UD F²'B² UD' F²'B² D² (5,14) UD F²'B² UD' F²'B² D² (5,14) |
                                          |
   F² R² F²'B² R² F² R²'L² (6,16) F² R² F²'B² R² F² R²'L² (6,16) |
                                            |
   F²'B² UD' F²'B² U'D (4,12) F²'B² UD' F²'B² U'D (4,12) |
                                                   |
   FB RL FB R'L' F'B' R'L' U' F²'B² R²'L² D' (10,22) FB RL FB R'L' F'B' R'L' U' F²'B² R²'L² D' (10,22) |
                                                |
   FB R F²'B² U²'D² L' F'B' U² R'L' F² R'L' U² (11,24) FB R F²'B² U²'D² L' F'B' U² R'L' F² R'L' U² (11,24) |
                                                          |
   F R F L D F' L' FB' R'L F'B R F U L' B' L F (17,20) F R F L D F' L' FB' R'L F'B R F U L' B' L F (17,20) |
                                                  |
   F² U F B D² R² B² D² L² F'B' U² R² D F² (14,26) F² U F B D² R² B² D² L² F'B' U² R² D F² (14,26) |
                                            |
   U² F²'B² R²'L² D² (4,12) U² F²'B² R²'L² D² (4,12) |
                                         |
   F²'B² R²'L² (2,8) F²'B² R²'L² (2,8) |
                                                          |
   F U' B' D' F² U' F' U'D² F U² F' D' F U' B' L² D' (17,22) F U' B' D' F² U' F' U'D² F U² F' D' F U' B' L² D' (17,22) |
                                                 |
   F² R²'L² U RL F² UD L² UD B² RL U B² (12,24) F² R²'L² U RL F² UD L² UD B² RL U B² (12,24) |
                                                    |
   F² U FB D² FB R²'L² D' B² U'D' R² U'D' (11,22) F² U FB D² FB R²'L² D' B² U'D' R² U'D' (11,22) |
                                                         |    U F R U F'B² R F D' R' F' L' F² R D RL²' D² (16,22) U F R U F'B² R F D' R' F' L' F² R D RL²' D² (16,22) |                                                    | |
   U² F U² R'L F² U' B² R'L D² B' U²'D² B D² (13,24) U² F U² R'L F² U' B² R'L D² B' U²'D² B D² (13,24) |
                                                    |
   F U² R'L F² U' B² R'L D² B' U²'D² B (11,20) F U² R'L F² U' B² R'L D² B' U²'D² B (11,20) |
                                                     |
   FB R F² UD' L² F' UD L U'D RL' U' L² (12,20) FB R F² UD' L² F' UD L U'D RL' U' L² (12,20) |
                                                      |
   FB R FB' R'L B' U'D' R' U² B² U² RL FB' U (13,22) FB R FB' R'L B' U'D' R' U² B² U² RL FB' U (13,22) |
                                                    |
   F UD FB' U² R'L B' R'L FB' R' U'D' F' (11,18) F UD FB' U² R'L B' R'L FB' R' U'D' F' (11,18) |
                                                 |
   F R² UD R U'D F² RL' D RL' U² R² F' (12,20) F R² UD R U'D F² RL' D RL' U² R² F' (12,20) |
                                                     |
   F RL U B² R² UD' R' L' UD' R U'D' L² F' (12,20) F RL U B² R² UD' R' L' UD' R U'D' L² F' (12,20) |
                                                |
   F R² UD' B² R²'L F²'B² L' B² U'D R² F (11,22) F R² UD' B² R²'L F²'B² L' B² U'D R² F (11,22) |
                                                     |
   FB R FB' R'L B' R² U'D' R²'L U² FB' R² U (12,22) FB R FB' R'L B' R² U'D' R²'L U² FB' R² U (12,22) |
                                                         |
   F R' F R²L' B' D R' U' B L F' R² B² L² D' F² (16,22) F R' F R²L' B' D R' U' B L F' R² B² L² D' F² (16,22) |
                                            |
   F²'B² UD' F²'B² UD' (4,12) F²'B² UD' F²'B² UD' (4,12) |
                                             |
   UD F²'B² UD' F²'B² U² (5,14) UD F²'B² UD' F²'B² U² (5,14) |
                                                    |
   FB R F²'B² U² RL B² RL U² L FB R² (11,22) FB R F²'B² U² RL B² RL U² L FB R² (11,22) |
                                                  |
   FB R F² R² B² U² L² F² R² U² L' FB L² (13,24) FB R F² R² B² U² L² F² R² U² L' FB L² (13,24) |
                                                   |
   FB R'L' FB U F²'B² R²'L² D RL F'B' RL (10,22) FB R'L' FB U F²'B² R²'L² D RL F'B' RL (10,22) |
                                                |
   FB R F²'B² U²'D² L' F'B' U² R'L' F² R'L' D² (11,24) FB R F²'B² U²'D² L' F'B' U² R'L' F² R'L' D² (11,24) |
                                            |
   U² F²'B² R²'L² U² (4,12) U² F²'B² R²'L² U² (4,12) |
                                                    |
   FB R F² R'L' D² F²'B² RL B² L FB L² (11,22) FB R F² R'L' D² F²'B² RL B² L FB L² (11,22) |
                                                 |
   F² U F² R U² F²'B² R²'L² U² L B² D B² (12,24) F² U F² R U² F²'B² R²'L² U² L B² D B² (12,24) |
                                                            |
   F U' F L' F' D F' R' L U'D F R' L D R' D L' F' L U' L (19,22) F U' F L' F' D F' R' L U'D F R' L D R' D L' F' L U' L (19,22) |
                                                  |
   F B R F²'B² U²'D² L' U²R² U² FB U² R² U² R² (13,28) F B R F²'B² U²'D² L' U²R² U² FB U² R² U² R² (13,28) |
                                                    |
   F U² R'L B² U F²'B² U' F² R'L U² B' (11,20) F U² R'L B² U F²'B² U' F² R'L U² B' (11,20) |
                                                     |
   F UD R U'D R'L U F'B R² F'B R'L U² B' (12,20) F UD R U'D R'L U F'B R² F'B R'L U² B' (12,20) |
                                                    |
   F R F² R U L D B² U' R' D F²'B² D² L² B' (15,22) F R F² R U L D B² U' R' D F²'B² D² L² B' (15,22) |
                                                         |
   F RL U R' D' F'B' U L F'B' R F'B' D' F R U R (16,20) F RL U R' D' F'B' U L F'B' R F'B' D' F R U R (16,20) |
                                                      |
   F U' L U L F² D B² U'D B D' R' B' L² U' B L² (17,22) F U' L U L F² D B² U'D B D' R' B' L² U' B L² (17,22) |
                                                      |
   FB R FB' R'L B' U'D' L FB' D² F² L² F² U' (13,22) FB R FB' R'L B' U'D' L FB' D² F² L² F² U' (13,22) |
                                                    |
   F R²'L² F' U² R'L B² D F² RL' U² B' (20,14 ) F R²'L² F' U² R'L B² D F² RL' U² B' (20,14 ) |
                                                     |
   F UD FB' U² R'L B' R'L FB' R' U'D' F' U²'D² (12,22) F UD FB' U² R'L B' R'L FB' R' U'D' F' U²'D² (12,22) |
                                                  |
   U² F R²'L² F' U² R'L B² D F² RL' U² B' D² (13,24) U² F R²'L² F' U² R'L B² D F² RL' U² B' D² (13,24) |
                                                      |
   FB R FB' R'L B' U'D' L FB' D² B² L² B² U' (13,22) FB R FB' R'L B' U'D' L FB' D² B² L² B² U' (13,22) |
                                                     |
   FB R FB' R'L B' R² U'D' L D² FB' L² U' (12,20) FB R FB' R'L B' R² U'D' L D² FB' L² U' (12,20) |
                                              |
   FB UD RL FB UD RL (6,12) FB UD RL FB UD RL (6,12) |
                                               |
   FB UD RL F'B' U'D' R'L' U²'D² (7,16) FB UD RL F'B' U'D' R'L' U²'D² (7,16) |
                                                   |
   U F² RL' FB' U² B² RL D² R² D' (10,18) U F² RL' FB' U² B² RL D² R² D' (10,18) |
                                                   |
   U F² R'L F'B D² B² R'L' U² R² D' (10,18) U F² R'L F'B D² B² R'L' U² R² D' (10,18) |
                                                 |
   FB U² FB RL' FB D² R'L' F² U' D' (9,18) FB U² FB RL' FB D² R'L' F² U' D' (9,18) |
                                               |
   FB' RL F'B R² B² L² U'D' L² F² R² (10,20) FB' RL F'B R² B² L² U'D' L² F² R² (10,20) |
                                                |
   FB UD RL FB UD' R²'L² D² R'L' (8,18) FB UD RL FB UD' R²'L² D² R'L' (8,18) |
                                               |
   FB' RL F'B R² F² R² UD R² B² R² (10,20) FB' RL F'B R² F² R² UD R² B² R² (10,20) |
                                                |
   U F² RL FB RL UD F² U' (8,14) U F² RL FB RL UD F² U' (8,14) |
                                                |
   U F² R'L' F'B' R'L' U'D' F² U' (8,14) U F² R'L' F'B' R'L' U'D' F² U' (8,14) |
                                                       |
   F U R F'B U²'D F' U'D R F U'D L' U' F' R²'L² (14,22) F U R F'B U²'D F' U'D R F U'D L' U' F' R²'L² (14,22) |
                                                        |
   F R B D F U B R'L F' D' FB' R' B R² D (15,18) F R B D F U B R'L F' D' FB' R' B R² D (15,18) |
                                                      |
   U F' UD' F'B D F B R' U² F'B L² D' R'L' U (13,20) U F' UD' F'B D F B R' U² F'B L² D' R'L' U (13,20) |
                                                  |
   FB' R U² R D² R' UD' F R² D² F R' L' U²D' (13,22) FB' R U² R D² R' UD' F R² D² F R' L' U²D' (13,22) |
                                                      |
   F R² U'D B² L U'D' FB R² B UD' FB' U R'L' (13,22) F R² U'D B² L U'D' FB R² B UD' FB' U R'L' (13,22) |
                                                        |
   F U L U F' R'L' U B' L' F' U'D B' U'D' R² U'D' (15,20) F U L U F' R'L' U B' L' F' U'D B' U'D' R² U'D' (15,20) |
                                                      |
   U F RL' F'B L' U'D' F D² RL' F² D RL U (13,20) U F RL' F'B L' U'D' F D² RL' F² D RL U (13,20) |
                                                   |
   U FB R' U² F² R' UD' B L² F' R² B' R'L D² (14,22) U FB R' U² F² R' UD' B L² F' R² B' R'L D² (14,22) |
                                                     |
   F² RL' U² B R'L' B² D' RL' U'D R FB D (12,20) F² RL' U² B R'L' B² D' RL' U'D R FB D (12,20) |
                                              |
   FB UD RL F'B' U'D' R'L' (6,12) FB UD RL F'B' U'D' R'L' (6,12) |
                                               |
   FB UD RL FB UD RL U²'D² (7,14) FB UD RL FB UD RL U²'D² (7,14) |
                                                 |
   U F² UD' F'B' R'L' F'B' D² B² U' (9,16) U F² UD' F'B' R'L' F'B' D² B² U' (9,16) |
                                                 |
   U F² UD' FB RL FB U²B² U' (9,16) U F² UD' FB RL FB U²B² U' (9,16) |
                                                          |
   F U' B' L' B' U F UD' L D R' B' R' D' L D² (16,18) F U' B' L' B' U F UD' L D R' B' R' D' L D² (16,18) |
                                               |
   FB' RL F'B R² F² R² U'D' L² F² L² (10,20) FB' RL F'B R² F² R² U'D' L² F² L² (10,20) |
                                                |
   FB UD RL F B U² F²'B² UD' R'L' (8,18) FB UD RL F B U² F²'B² UD' R'L' (8,18) |
                                               |
   FB' RL F'B R² B² L² UD R² B² L² (10,20) FB' RL F'B R² B² L² UD R² B² L² (10,20) |
                                                |
   U FB R'L' UD F'B' UD F'B' U' (8,14) U FB R'L' UD F'B' UD F'B' U' (8,14) |
                                            |
   U F² R'L' F'B' R'L' U'D' F² UD²' (8,16) U F² R'L' F'B' R'L' U'D' F² UD²' (8,16) |
                                                |
   U FB RL U'D' FB U'D' F'B' U' (8,14) U FB RL U'D' FB U'D' F'B' U' (8,14) |
                                            |
   U F² RL FB RL UD F² UD²' (8,16) U F² RL FB RL UD F² UD²' (8,16) |
                                                      |
   F R² U'D B² L F'B' U' RL' U'D R' B² RL U'D' (13,22) F R² U'D B² L F'B' U' RL' U'D R' B² RL U'D' (13,22) |
                                                      |
   F R² U'D B² L U'D' FB R² F U'D F'B D R'L' (13,22) F R² U'D B² L U'D' FB R² F U'D F'B D R'L' (13,22) |
                                                      |
   U F' R U L U' R F' U' R U RL' B' R' L' F' D (18) U F' R U L U' R F' U' R U RL' B' R' L' F' D (18) |
                                                  |
   FB' R U² R D² R' UD' F R² D² F R'L' D (13,20) FB' R U² R D² R' UD' F R² D² F R'L' D (13,20) |
                               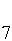                           |
   F R' F' R UD' F' D' F' R' U' L' B' U L' F' D' L (17,18) F R' F' R UD' F' D' F' R' U' L' B' U L' F' D' L (17,18) |
                                                   |
   U FB R' U² F² R' UD' F U² F' D² F' R'L U² (14,22) U FB R' U² F² R' UD' F U² F' D² F' R'L U² (14,22) |
                             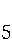                           |
   F U L U F' R'L' U B' L' F' U'D B' U'D' R² UD (15,20) F U L U F' R'L' U B' L' F' U'D B' U'D' R² UD (15,20) |
                                                     |
   F U R D' R² U² F UD B D² L² U' L D B RL (16,22) F U R D' R² U² F UD B D² L² U' L D B RL (16,22) |
                                                       |
   U²'D² L F² U'D R² B U'D' RL F² R UD' R'L U F'B' (14,26) U²'D² L F² U'D R² B U'D' RL F² R UD' R'L U F'B' (14,26) |
                                                      |
   F U² RL D F² U R² D F² D F'B' U² L F² R² B² U'D (17,28) F U² RL D F² U R² D F² D F'B' U² L F² R² B² U'D (17,28) |
                                                      |
   FB' R F² L B² R' U'D F L² U² F R'L' U (13,20) FB' R F² L B² R' U'D F L² U² F R'L' U (13,20) |
                                                     |
   FB' U² L FB L² U FB' U'D B' R'L' U R² (12,20) FB' U² L FB L² U FB' U'D B' R'L' U R² (12,20) |
                                                |
   FB UD R'L' U² F'B' U'D' RL U² (8,16) FB UD R'L' U² F'B' U'D' RL U² (8,16) |
                                                |
   FB UD R'L' U² FB UD R'L' D² (8,16) FB UD R'L' U² FB UD R'L' D² (8,16) |
                                                   |
   FB RL FB R² U' F²'B² R²'L² D' R² U'D' (10,22) FB RL FB R² U' F²'B² R²'L² D' R² U'D' (10,22) |
                                                         |
   F R' B L U B R UD L F D R F L' B R²'L² (16,20) F R' B L U B R UD L F D R F L' B R²'L² (16,20) |
                                               |
   F² RL FB RL U D F² U' F²'B² R²'L² D' (10,22) F² RL FB RL U D F² U' F²'B² R²'L² D' (10,22) |
                                               |
   FB UD R'L' F'B' UD RL U²'D² (7,16) FB UD R'L' F'B' UD RL U²'D² (7,16) |
                                              |
   FB UD R'L' FB U'D' R'L' (6,12) FB UD R'L' FB U'D' R'L' (6,12) |
                                                      |
   F RL B' R'L' B U'D' F'B' U'D' F' R'L' F RL B' (13,20) F RL B' R'L' B U'D' F'B' U'D' F' R'L' F RL B' (13,20) |
                                                |
   FB RL FB UD' F² U' F²'B² R²'L² D' F² U² (11,24) FB RL FB UD' F² U' F²'B² R²'L² D' F² U² (11,24) |
                                                    |
   FB R F'B' LR' FB RL UD FB R FB L² (11,20) FB R F'B' LR' FB RL UD FB R FB L² (11,20) |
                                                 |
   F² U FB' U² RL FB' L² F² U'D' B² D' F² (12,22) F² U FB' U² RL FB' L² F² U'D' B² D' F² (12,22) |
                                                       |
   F UD' F UD' R² U² L' F² UD' L² F RL U B' (14,22) F UD' F UD' R² U² L' F² UD' L² F RL U B' (14,22) |
                                                        |
   F R B L D F'B L' U'D F'B² UD' B' D' R' B' U' (15,20) F R B L D F'B L' U'D F'B² UD' B' D' R' B' U' (15,20) |
                                                           |
   F R' U'D' R D' F' D' R U'D' L U' B' U' L U'D' L' B (17,20) F R' U'D' R D' F' D' R U'D' L U' B' U' L U'D' L' B (17,20) |
                                                   |
   FB' R D² L F²'B² R' F² R' U'D B U² F² R'L D' (15,24) FB' R D² L F²'B² R' F² R' U'D B U² F² R'L D' (15,24) |
                                                     |
   FB' U² RF B R² U'D² FB' U'D B' R'L' U L² (12,22) FB' U² RF B R² U'D² FB' U'D B' R'L' U L² (12,22) |
                                                      |
   F R U'D² F'B R' B' RL' D B RL' U' L' F' (13,18) F R U'D² F'B R' B' RL' D B RL' U' L' F' (13,18) |
                                                      |
   F U² R'L F² U RL F'B' D² F' R'L FB' R' UD (13,22) F U² R'L F² U RL F'B' D² F' R'L FB' R' UD (13,22) |
                                                            |
   F RL U' R U² B R' F L B' L' B L D' FB' U' F D' F' (19,22) F RL U' R U² B R' F L B' L' B L D' FB' U' F D' F' (19,22) |
                                                   |
   FB' R UD' B² R² B' RL' D F² D F²'B² U' L² D' (14,24) FB' R UD' B² R² B' RL' D F² D F²'B² U' L² D' (14,24) |
                                                     |
   FB' U² L F'B' D' F'B U'D B U² RL D L² (12,20) FB' U² L F'B' D' F'B U'D B U² RL D L² (12,20) |
                                                |
   FB UD R'L' U² FB UD R'L' U² (8,16) FB UD R'L' U² FB UD R'L' U² (8,16) |
                                                |
   FB UD R'L' U² F'B' U'D' RL D² (8,16) FB UD R'L' U² F'B' U'D' RL D² (8,16) |
                                                      |
   F² U RL' D² FB RL' B² R² U'D' L² D' B² (12,22) F² U RL' D² FB RL' B² R² U'D' L² D' B² (12,22) |
                                                   |
   FB RL FB R² U' F²'B² R²'L² D' R² UD (10,22) FB RL FB R² U' F²'B² R²'L² D' R² UD (10,22) |
                    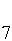                            |
   FB UD R'L' FB U'D' R'L' U²'D² (7,16) FB UD R'L' FB U'D' R'L' U²'D² (7,16) |
                                              |
   FB UD R'L' F'B' UD RL (6,12) FB UD R'L' F'B' UD RL (6,12) |
                                                    |
   FB R FB RL' F'B' R'L' UD F'B' L FB R² (11,20) FB R FB RL' F'B' R'L' UD F'B' L FB R² (11,20) |
                                                 |
   F² U FB' U² RL FB' L² F² UD F² D' B² (12,22) F² U FB' U² RL FB' L² F² UD F² D' B² (12,22) |
                                                    |
   FB RL FB UD' F² U' F²'B² R²'L² D' F² D² (11,24) FB RL FB UD' F² U' F²'B² R²'L² D' F² D² (11,24) |
                                                      |
   FB R FB' R'L F L² FB U'D' L D² FB' L² D (13,22) FB R FB' R'L F L² FB U'D' L D² FB' L² D (13,22) |
                             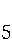                           |
   FB R² FB U' FB' D' L' U' B R'L' D' B L B D (15,20) FB R² FB U' FB' D' L' U' B R'L' D' B L B D (15,20) |
                                                     |
   FB' U² R FB R² U F'B U'D F' R'L' U R² (12,20) FB' U² R FB R² U F'B U'D F' R'L' U R² (12,20) |
                                                            |
   F RL' U' R² D B' L' B' D B' U' F D B' D R U R' U'D (19,22) F RL' U' R² D B' L' B' D B' U' F D B' D R U R' U'D (19,22) |
                                                   |
   FB' R UD' F L² F R²'L² B' D² F' RL' U L² U² (14,24) FB' R UD' F L² F R²'L² B' D² F' RL' U L² U² (14,24) |
                                                       |
   F RL' B RL' U² R² D' F² R'L D² F UD R F' (14,22) F RL' B RL' U² R² D' F² R'L D² F UD R F' (14,22) |
                                                     |
   FB' U² R FB R² D FB' UD' F²'B R'L' U R² (12,22) FB' U² R FB R² D FB' UD' F²'B R'L' U R² (12,22) |
                                                         |
   F R' D' R F R'L² U B U' R' U R'L' U'D' F'B' D F² (16,22) F R' D' R F R'L² U B U' R' U R'L' U'D' F'B' D F² (16,22) |
                                                   |
   FB R' F² U² R' U'D B R² B' U² F' U²'D² RL' D (14,24) FB R' F² U² R' U'D B R² B' U² F' U²'D² RL' D (14,24) |
 |

